1. Premesse allo studio
Abbiamo visto che si studia una quantità di fluido:
- che non presenta mai discontinuità;
- che non ha variazione di massa m;
- che presenta in tutti i punti la stessa densità cioè occupa sempre lo stesso volume V.

2. Definizione di Volume
Dalla geometria di base, il VOLUME di un solido è dato dal prodotto dell'area di base per l'altezza per cui, in geometria, si calcola con la seguente formula:
V = prodotto tra un'area S e una lunghezza l
(formula n.1)
per cui il VOLUME si misura in m² × m = m³

3. Definizione di Portata
Dalla fisica la PORTATA si definisce come il rapporto fra il volume V di fluido ed il tempo t che impiega quel volume ad attraversare una sezione del condotto:
q = rapporto tra un volume V ed un tempo t
(formula n.2)
per cui la PORTATA si misura in m³/s

4. Derivazione della formula
Partendo dalle formule:
- V = S × l (formula n.1)
- q = V / t (formula n.2)
Sostituendo nella formula n.2 il Volume così come calcolato nella formula n.1 si ha:
q = V / t = S × l / t
formula nella quale il rapporto l / t (lunghezza diviso tempo) è una velocità per cui:
formula nella quale si vede che la PORTATA è anche pari al PRODOTTO DI UN'AREA S PER UNA VELOCITÀ v.

5. Proporzionalità inversa
Con le ipotesi fatte all'inizio (fluido a densità costante) si capisce come LA PORTATA SIA COSTANTE QUALUNQUE SIA LA SEZIONE DEL CONDOTTO e dalla formula ora vista:
se il prodotto deve essere costante all'aumentare di S deve diminuire v (e viceversa).
S e v sono inversamente proporzionali.

6. Rappresentazione grafica
Il tutto si può rappresentare con questa figura:
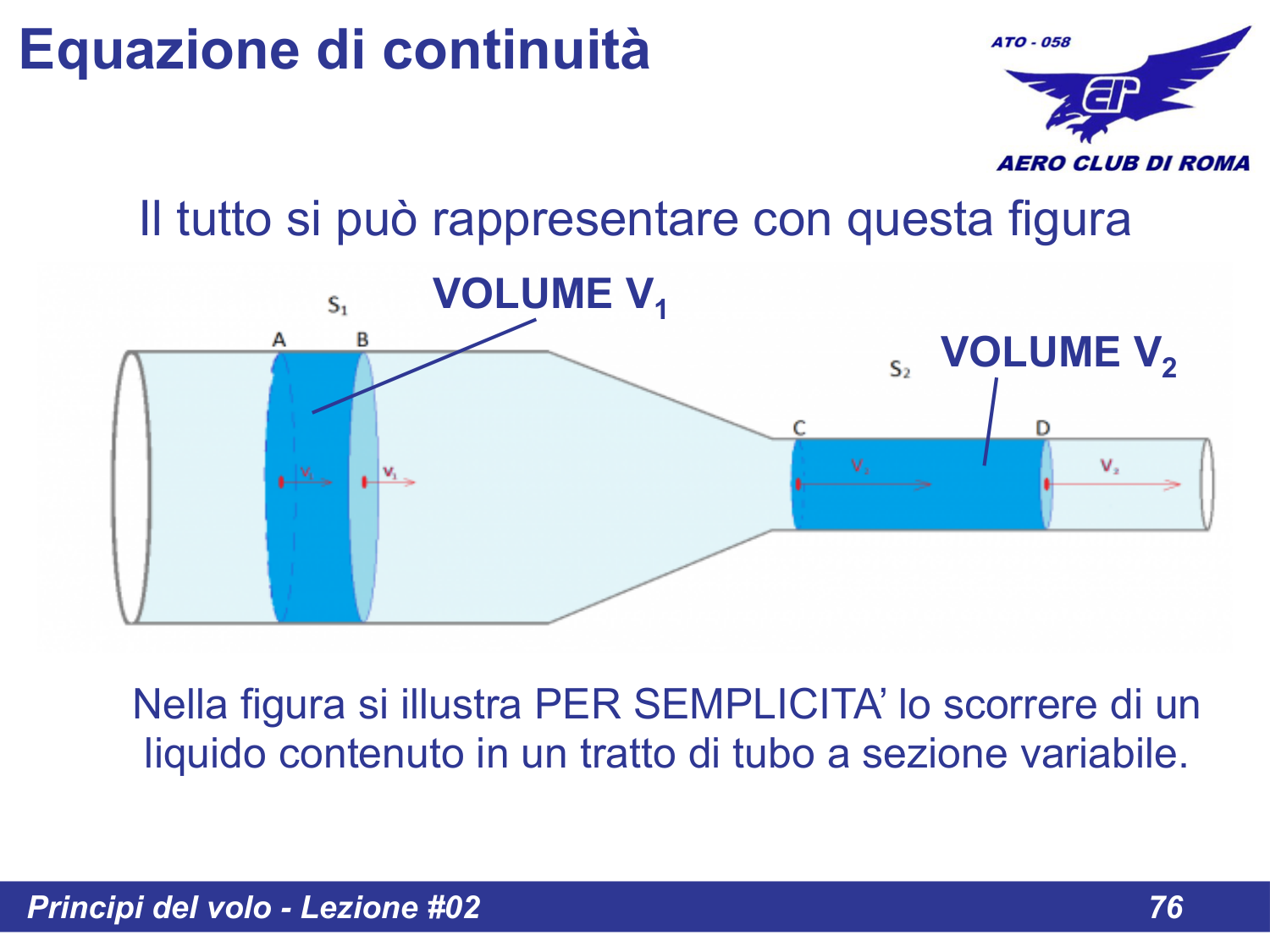
Nella figura si illustra PER SEMPLICITÀ lo scorrere di un liquido contenuto in un tratto di tubo a sezione variabile.
Per le ipotesi fatte all'inizio, il volume V₁ di fluido contenuto fra le sezioni A e B è uguale al volume V₂ di fluido contenuto fra le sezioni C e D cioè SI MANTIENE INALTERATA LA PORTATA.
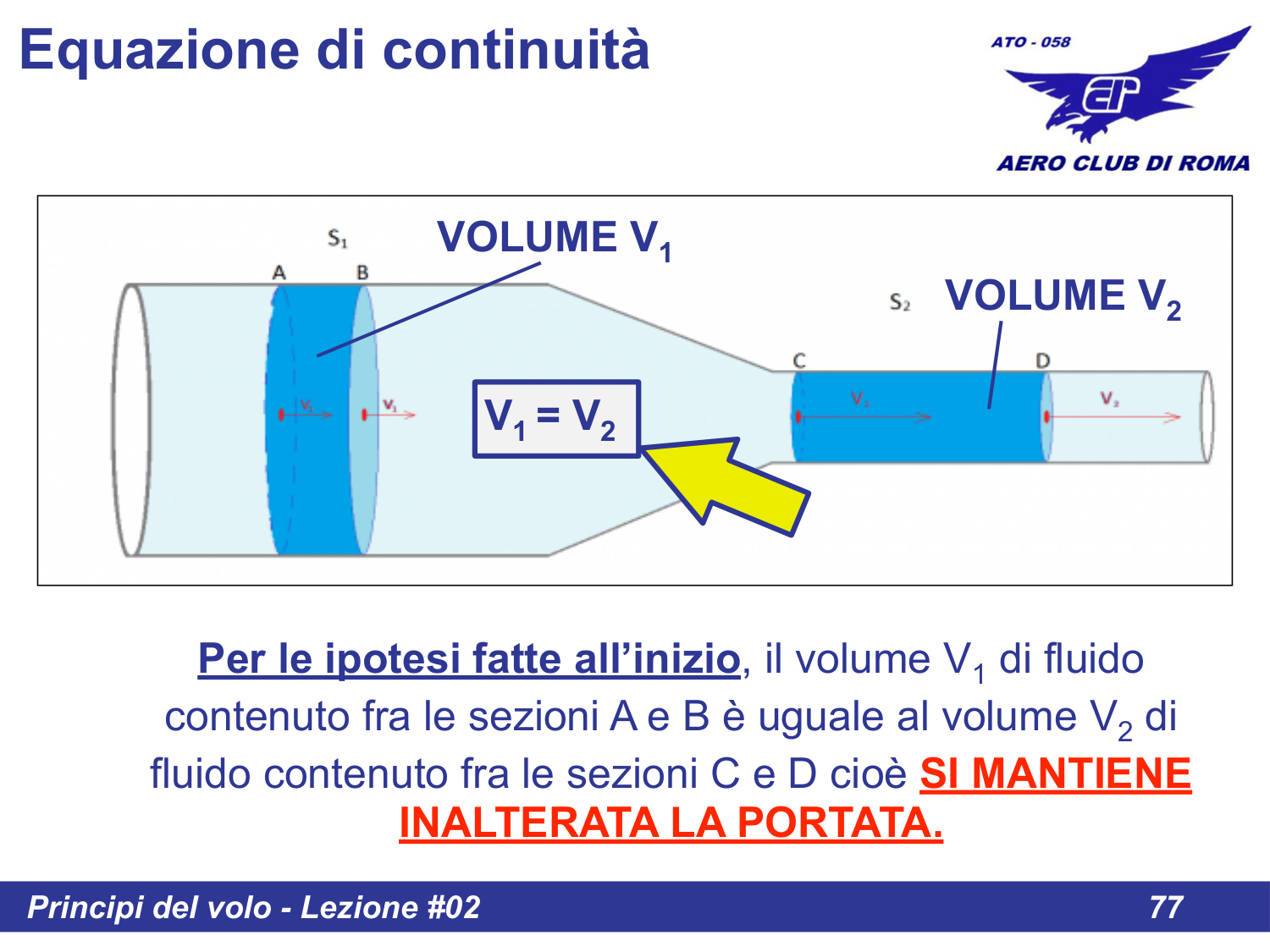
7. Equazione di Continuità
EQUAZIONE DI CONTINUITÀ
SEZIONE E VELOCITÀ SONO INVERSAMENTE PROPORZIONALI
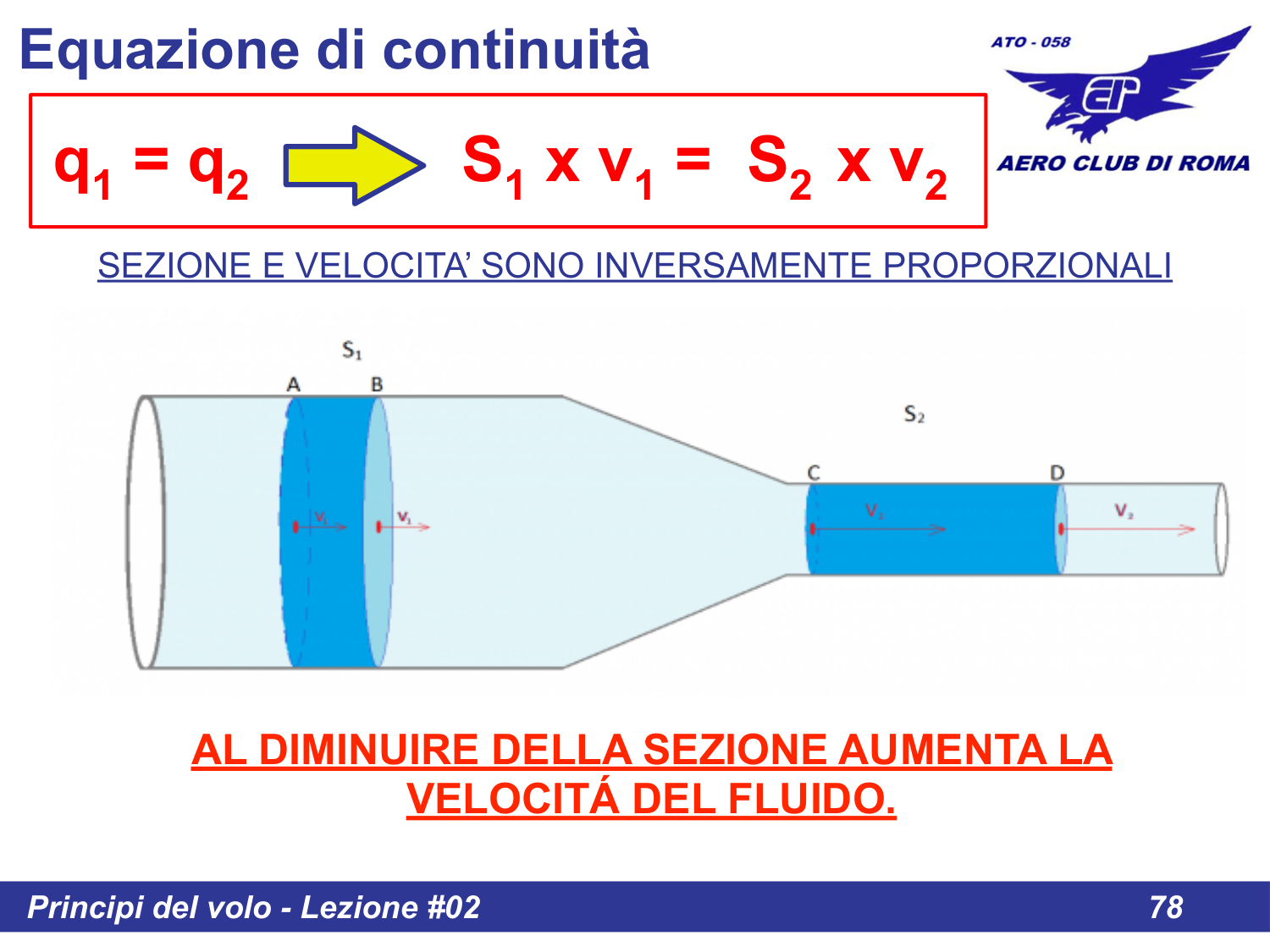
AL DIMINUIRE DELLA SEZIONE AUMENTA LA VELOCITÀ DEL FLUIDO
| Sezione | Velocità | Portata |
|---|---|---|
| S₁ (grande) | v₁ (bassa) | q = costante |
| S₂ (piccola) | v₂ (alta) | q = costante |
8. Applicazione pratica
L'equazione di continuità trova applicazione in molti contesti reali. Un esempio pratico è il flusso d'aria attorno a un'automobile:
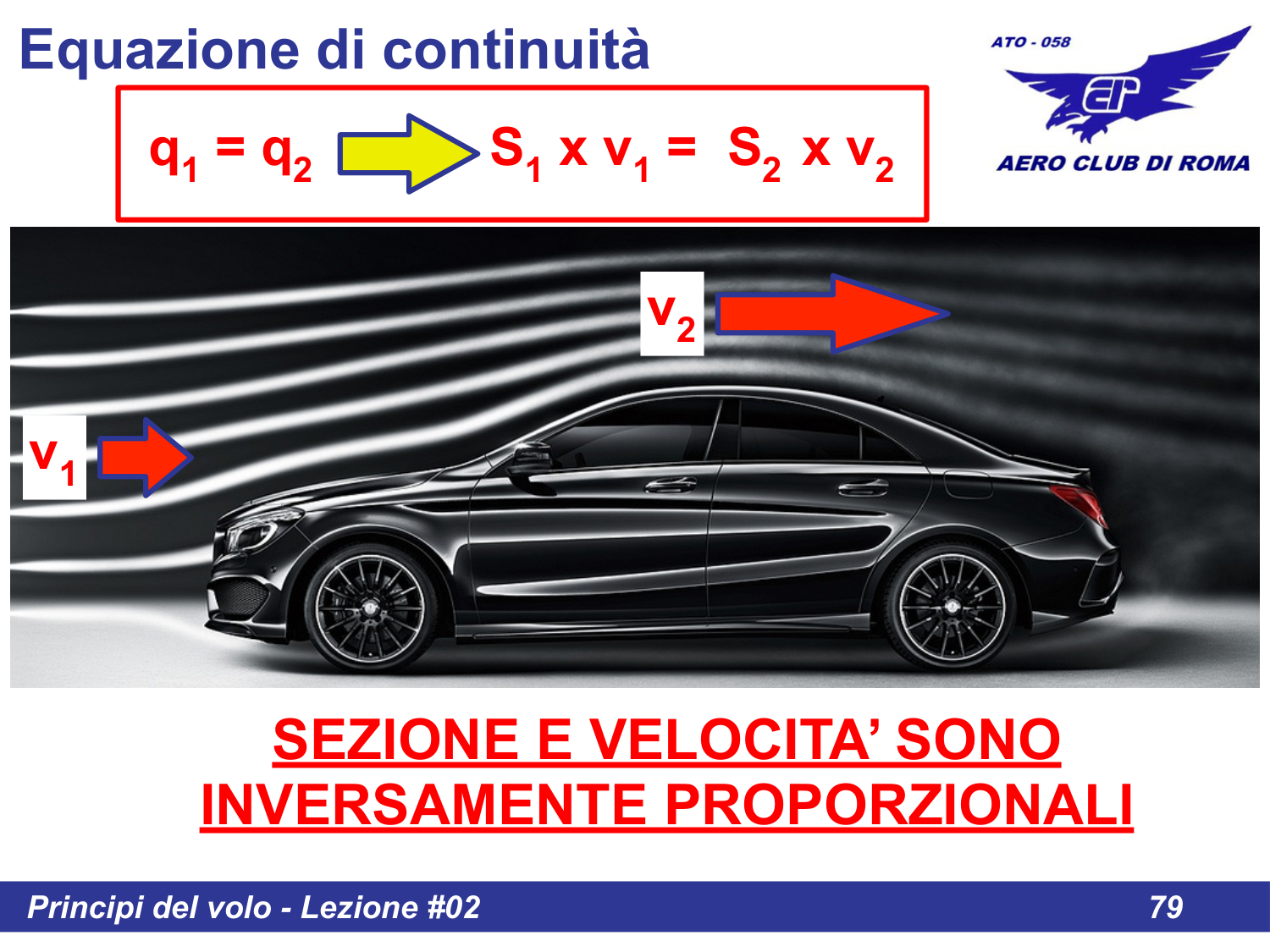
Nella figura si vede come l'aria che passa sopra e sotto la vettura:
- v₁ = velocità dell'aria in arrivo (sezione libera, ampia)
- v₂ = velocità dell'aria sopra la vettura (sezione ristretta, quindi velocità maggiore)
Riepilogo formule
| Formula | Nome | Unità di misura |
|---|---|---|
| V = S × l | Volume | m³ |
| q = V / t | Portata (definizione) | m³/s |
| q = S × v | Portata (formula alternativa) | m³/s |
| S₁ × v₁ = S₂ × v₂ | Equazione di Continuità | m³/s |
Concetti chiave da ricordare:
- La portata è costante in tutto il condotto
- Sezione e velocità sono inversamente proporzionali
- Dove la sezione diminuisce, la velocità aumenta
- Dove la sezione aumenta, la velocità diminuisce