Equazione di Bernoulli ed Effetto Venturi

1. Introduzione

L'equazione di Bernoulli esprime LA LEGGE DI CONSERVAZIONE DELL'ENERGIA nel caso particolare dei fluidi.

Introduzione Equazione di Bernoulli — Principio fondamentale dell'equazione di Bernoulli

2. Ipotesi semplificative

Il fluido viene studiato ipotizzando alcune semplificazioni fondamentali:

Non è comprimibile (densità costante)
Scorre in un condotto indeformabile
È soggetto a una corrente stazionaria
portata costante cioè: q₁ = q₂ ossia S₁ × v₁ = S₂ × v₂
Non presenta attrito
nessun attrito tra le particelle e fra particelle e pareti (viscosità nulla)

Ipotesi semplificative — Le 4 ipotesi semplificative per lo studio dei fluidi

3. Premesse allo studio

Il 2° Principio della Dinamica

Si può enunciare in vari modi. Ad esempio: Se ad un corpo di massa m si applica una forza F, il corpo subisce una accelerazione a (a = variazione della velocità v).

Quindi la FORZA F è il prodotto tra una MASSA m e una ACCELERAZIONE a:

F = m × a

(formula n.1)

La FORZA si misura in kg × m/s² = N (newton)

2° Principio della Dinamica — Il secondo principio della dinamica

Definizione di DENSITÀ

Dalla fisica la DENSITÀ (ρ) si definisce come il rapporto tra la massa m di un corpo e il volume V occupato dal corpo stesso.

ρ = rapporto tra una massa m e volume V

ρ = m / V

(formula n.2)

La DENSITÀ si misura in kg/m³

Definizione di Densità — Definizione di densità

Definizione di PRESSIONE

Dalla fisica la PRESSIONE si definisce come il rapporto tra forza F che agisce perpendicolarmente su una superficie S e la superficie stessa.

p = rapporto tra una forza F e una superficie S

p = F / S

(formula n.3)

La PRESSIONE si misura in N/m² = Pa (pascal)

Definizione di Pressione — Definizione di pressione

4. Derivazione matematica

Partendo dalle formule:

F = m × a (formula n.1)
m = ρ × V (formula n.2)

Sostituendo nella formula n.2 il Volume così come calcolato nella formula n.1 si ha:

p = F / S = m × a / S = ρ × V × a / S

formula nella quale l'accelerazione a è a sua volta definita con a = l / t²

p = ρ × V × l / t² × S con V / S che è una lunghezza

Si ha:

p = ρ × l × l / t² = ρ × l² / t² = ρ × v²

Derivazione matematica — Passaggi matematici per arrivare alla relazione p = ρv²

5. Equazione di Bernoulli

DANIEL BERNOULLI
STUDI DI FLUIDODINAMICA – ANNO 1738

Con opportuni passaggi matematici si ottiene:

Legge della conservazione dell'energia
(nel caso di una massa fluida in movimento)

P + ½ρv² + ρgh = cost

Equazione di Bernoulli completa — L'equazione di Bernoulli nella sua forma completa

Esempio: condotto idraulico

Esempio di un condotto idraulico con variazione di sezione e variazione di quota.

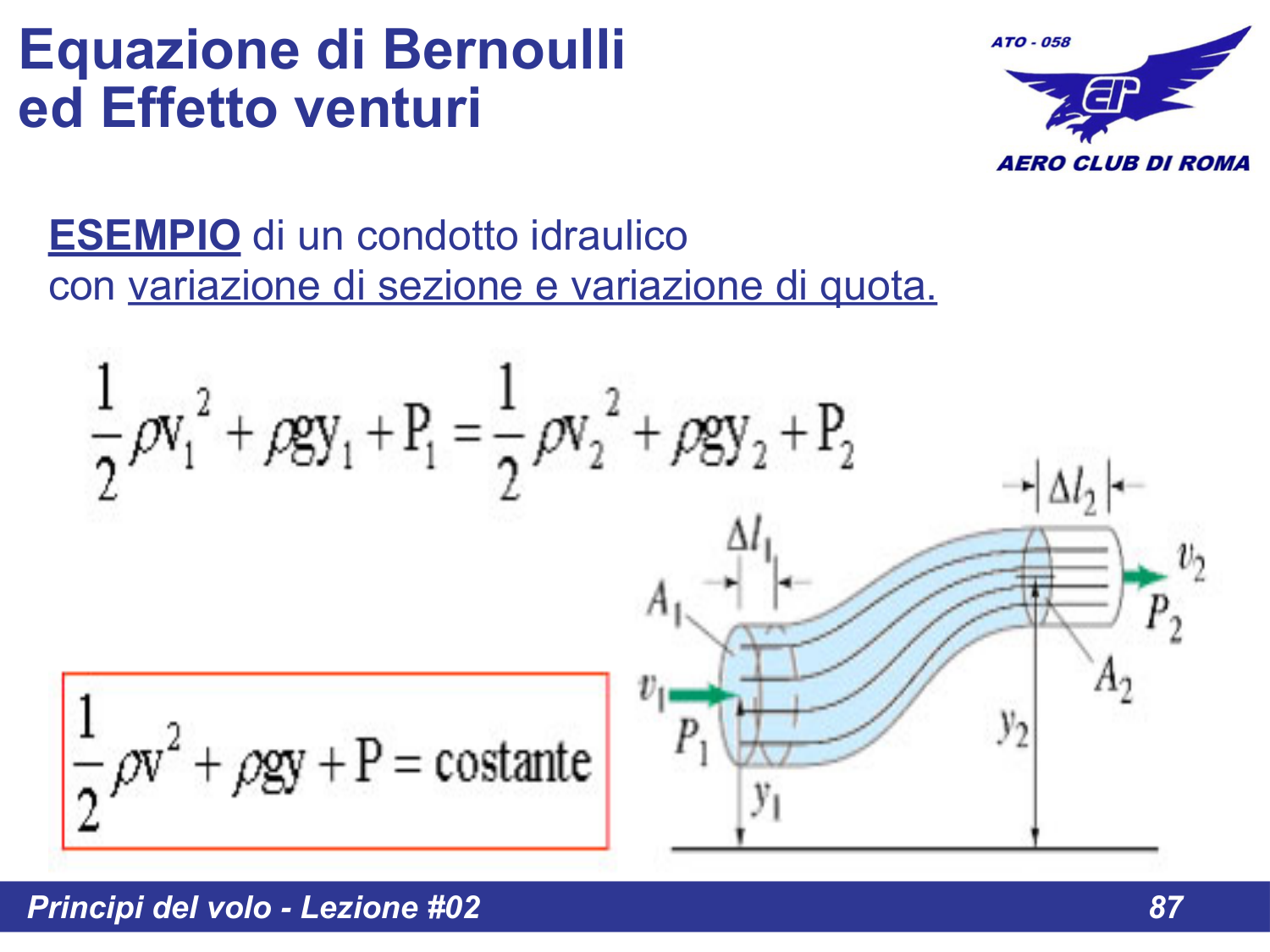
6. Significato dei termini

I 3 termini dell'equazione hanno il seguente significato:

P = PRESSIONE VERA (o piezometrica)

½ρv² = PRESSIONE DINAMICA (dovuta al moto del fluido)

ρgh = PRESSIONE DI ALTEZZA (dovuta alla variazione di quota)

Significato dei termini — I tre termini dell'equazione di Bernoulli e il loro significato

Termine	Nome	Descrizione
P	Pressione vera (piezometrica)	Pressione statica del fluido
½ρv²	Pressione dinamica	Dovuta al moto del fluido
ρgh	Pressione di altezza	Dovuta alla variazione di quota

7. Caso orizzontale (semiala)

È interessante per noi considerare il caso in cui l'equazione di Bernoulli viene applicata ad un condotto con asse orizzontale (cioè senza variazione di quota).

L'"Equazione di Bernoulli" viene modificata eliminando il termine ρgh

Caso condotto orizzontale — Eliminazione del termine ρgh per condotti orizzontali

È il caso di una semiala dove, per il tipo di movimento che ha il fluido rispetto ad essa, NON ESISTE il termine che tiene conto della variazione di quota.

L'"Equazione di Bernoulli"
P + ½ρv² + ~~ρgh~~ = cost
viene modificata eliminando il termine ρgh

P + ½ρv² = cost

Equazione semplificata per semiala — Equazione di Bernoulli semplificata per il caso della semiala

⚠️ IMPORTANTE !!!

La formula esprime il concetto che
quando la VELOCITÀ AUMENTA
(a causa di una diminuzione della sezione)
la PRESSIONE DIMINUISCE
e viceversa…

Concetto chiave velocità-pressione — Relazione inversa tra velocità e pressione

8. Effetto Venturi

Per riassumere il comportamento di un fluido in un condotto a sezione variabile:

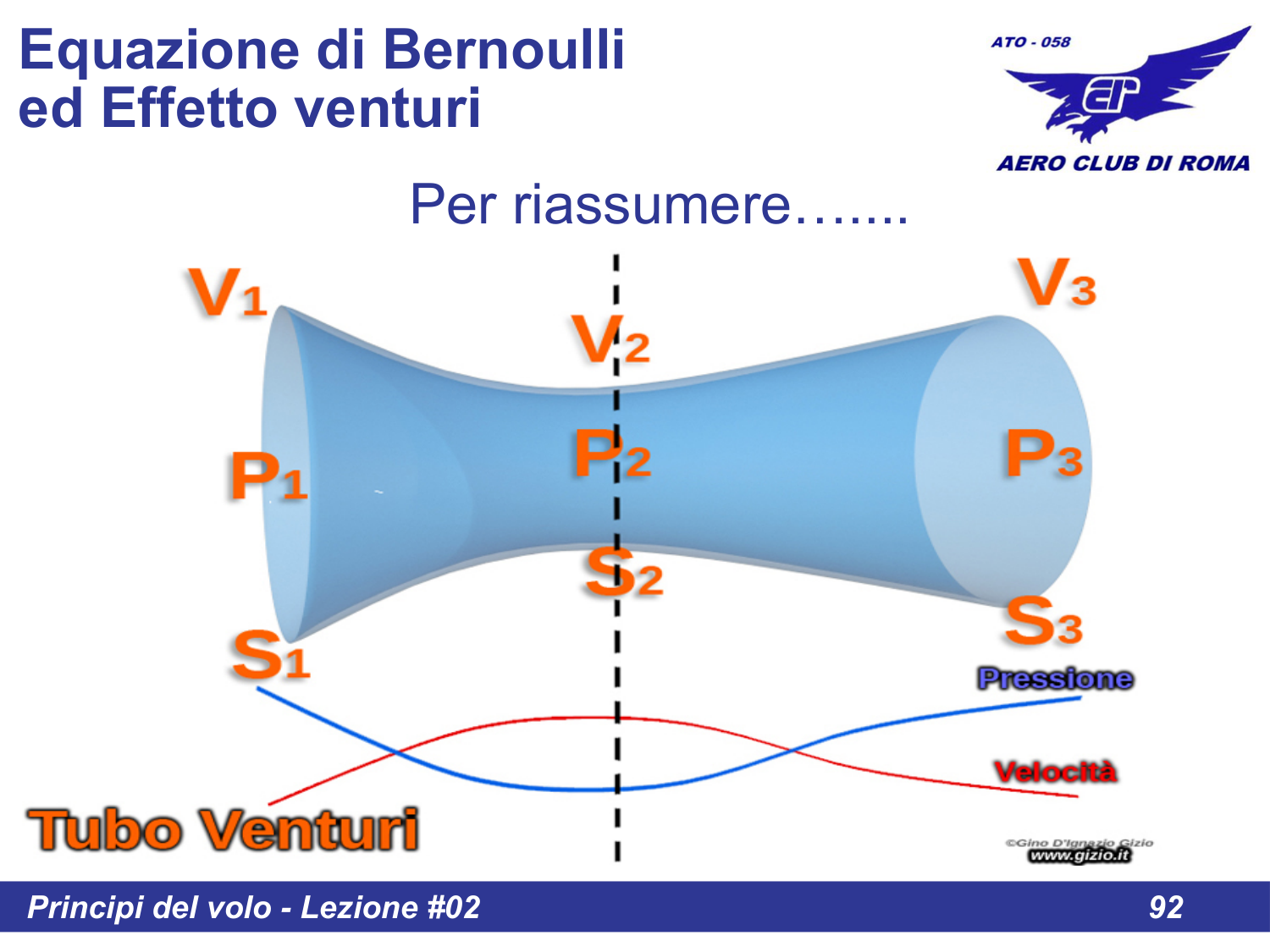
Nel Tubo di Venturi:

Dove la sezione diminuisce (S₂) → la velocità aumenta (V₂) → la pressione diminuisce (P₂)
Dove la sezione aumenta (S₁, S₃) → la velocità diminuisce (V₁, V₃) → la pressione aumenta (P₁, P₃)

Campo di flusso attorno al profilo alare

Distribuzione delle pressioni sul profilo

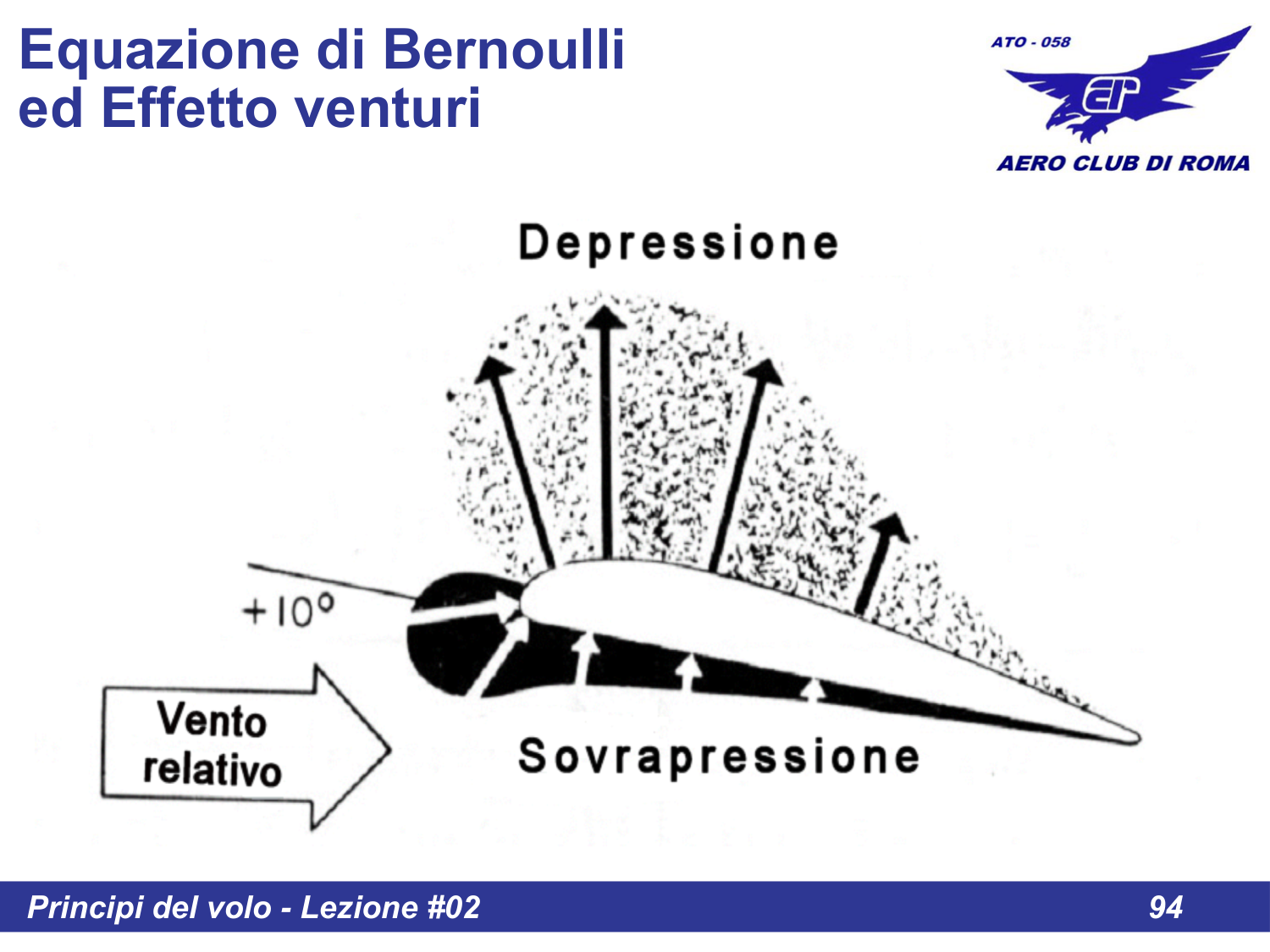
Depressione e Sovrapressione — Depressione sul dorso (estradosso) e sovrapressione sul ventre (intradosso) del profilo alare

Sul dorso (estradosso) del profilo: l'aria accelera → DEPRESSIONE

Sul ventre (intradosso) del profilo: l'aria rallenta → SOVRAPRESSIONE

La differenza di pressione tra intradosso ed estradosso genera la PORTANZA.

9. Applicazioni pratiche

Alcune conseguenze dell'EFFETTO VENTURI:

Esempi nella vita quotidiana:

Il fumo prodotto da una sigaretta in un'auto in movimento si allontana aprendo uno "spiraglio" di finestrino (l'aria esterna, più veloce, crea una depressione che "aspira" il fumo)
In caso di tornado/tromba d'aria le finestre di una abitazione esplodono verso l'esterno (la pressione interna alla casa rimane alta mentre all'esterno la velocità del vento crea una forte depressione)

Conseguenze Effetto Venturi — Esempi pratici dell'effetto Venturi

Riepilogo formule

Formula	Nome	Unità di misura
F = m × a	2° Principio della Dinamica	N (newton)
ρ = m / V	Densità	kg/m³
p = F / S	Pressione	Pa (pascal)
P + ½ρv² + ρgh = cost	Equazione di Bernoulli (completa)	Pa
P + ½ρv² = cost	Eq. Bernoulli (senza variazione quota)	Pa